深度优先搜索(DFS)算法从图G的初始节点开始,然后越来越深,直到找到目标节点或没有子节点的节点。该算法然后从死角回溯到尚未完全未探索的最新节点。
在DFS中使用的数据结构是堆栈。该过程类似于BFS算法。 在DFS中,通向未访问节点的边称为发现边,而通向已访问节点的边称为块边。
算法
第1步:为G中的每个节点设置STATUS = 1(就绪状态)
第2步:将起始节点A推入堆栈并设置其STATUS = 2(等待状态)
第3步:重复第4步和第5步,直到STACK为空
第4步:弹出顶部节点N.处理它并设置其STATUS = 3(处理状态)
第5步:将处于就绪状态(其STATUS = 1)的N的所有邻居推入堆栈并设置它们
STATUS = 2(等待状态)
[循环结束]
第6步:退出
示例:
考虑图G及其邻接列表,如下图所示。 通过使用深度优先搜索(DFS)算法计算从节点H开始打印图的所有节点的顺序。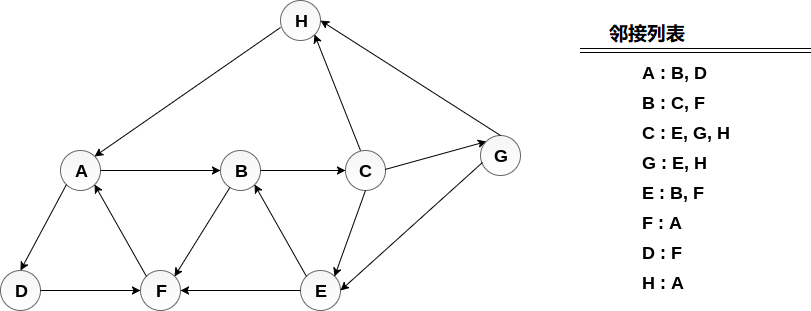
方案:
将H 推入堆栈 -
STACK : H
弹出是堆栈的顶部元素,即H,打印它并将H的所有邻居推送到处于就绪状态的堆栈上。
Print H
STACK : A
弹出堆栈的顶部元素,即A,打印它并将A的所有邻居推入堆栈中处于就绪状态。
Print A
Stack : B, D
弹出堆栈的顶部元素,即D,打印它并将D的所有邻居推入处于就绪状态的堆栈。
Print D
Stack : B, F
弹出堆栈的顶部元素,即F,打印它并将F的所有邻居推入处于就绪状态的堆栈。
Print F
Stack : B
弹出堆栈的顶部,即B并推送所有邻居。
Print B
Stack : C
弹出堆栈的顶部,即C并推送所有邻居。
Print C
Stack : E, G
弹出堆栈的顶部,即G并推送其所有邻居。
Print G
Stack : E
弹出堆栈的顶部,即E并推送其所有邻居。
Print E
Stack :
因此,堆栈现在变为空,并且遍历了图的所有节点。
图表的打印顺序为:
H → A → D → F → B → C → G → E
上一篇:
广度优先搜索(BFS)算法
下一篇:
生成树
